0 KiB
0 MiB
0 GiB
0 TiB
0 PiB
0 KB
0 MB
0 GB
0 TB
0 PB
N/A
N/A
N/A
N/A
N/A
How is it possible that "kilobyte" may represent two different values (1000 Bytes and 1024 Bytes)?
Up to the year 2000, if someone was to say "one kilobyte". By that they meant of value 210 or 1024. We can say that there was a good reason for that. Computers are based on binary system, base of the binary system is 2 since it has only two values 0 and 1. Base of decimal system, system we use in our every day life is 10. We know there are standardized values of prefixes that represent bigger values so we don't have to write all those zeroes at the end for large numbers. Now, if we are to get the value of the first prefix, kilo, we can write 103 or 1000 in decimal system. If we are to calculate that prefix value in binary system, the closest value to 1000 would be 1024. For example, 29 is 512, 210 is 1024. Which value of these two is closer to 1000? It is 1024. So 1024 or 210 was taken to represent the value of kilo in computer systems. That is reason why it was agreed at beginning for kilobyte to have value of 1024 bytes.
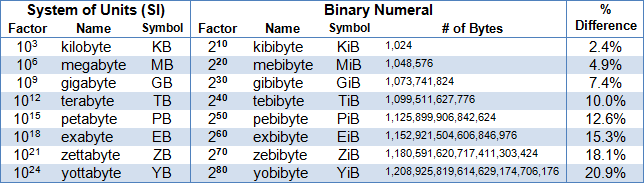
To fix the issue, in year 1999 IEC (International Electrotechnical Commission) suggested to change the names of units based on binary system. Base of binary system is 2, word that represent the value of two is "bi". So IEC suggested to change last two letters in standard prefix name with "bi". So, we got kilo as kibi. Kilobyte became kibibyte, megabyte became mebibyte and so on. These values have it's own abbreviations as well, kibibyte is KiB, megabyte is MiB. Notice the letter i in the abbreviated name. So, old value "10 KB" became "10 KiB".
Table bellow is showing some of these new values. These new values should be used.
| Name of unit | Simbol | Value |
|---|---|---|
| 1 kilobyte | 1 kB | 103 = 1000 bytes |
| 1 megabyte | 1 MB | 106 = 1000000 bytes |
| 1 gigabyte | 1 GB | 109 = 1000000000 bytes |
| 1 terabyte | 1 TB | 1012 = 1000000000000 bytes |
| 1 petabyte | 1 PB | 1015 = 1000000000000000 bytes |
| 1 kibibayte | 1 KiB | 210 = 1024 bytes |
| 1 mebibyte | 1 MiB | 220 = 1048576 bytes |
| 1 gibibyte | 1 GiB | 230 = 1073741824 bytes |
| 1 tebibyte | 1 TiB | 240 = 1099511627776 bytes |
| 1 pebibyte | 1 PiB | 250 = 1125899906842624 bytes |
We still have problems related to these notations, majority of people and even school books are still using those wrong values with base 2 when they write prefixes kilo, mega, giga and so on.
It seems like we are stack between values for "megabyte". Is it 1 000 000 bytes or 1 048 576 bytes? Since there is a huge difference between 'SI' and 'IEC' units, the confusion rises even bigger with larger capacity of disks. For example gibibyte is 7,4% larger than gigabyte, tebibyte is 10% larger than terabyte, and that is just a huge difference. Many people complain when they for example buy hard disk of 250 GB their OS (operating system) is showing only "232 GB". This is not manufacturer fault, and it is not a marketing trick. It is true that 250 gigabytes is equal to 232, but 232 gibibytes. We need to blame OS here, because it is still using that wrong notation.
Some OS's like windows are still using obsolete notation without proper IEC names for units, that confuses users. But, on the other hand some OS's like Linux are using the right notation, because of it's "open source" code policies.
All the manufacturers should use these new, corrected values with new names with Si abbreviations 'kB', 'MB' or IEC 'KiB', 'MiB' etc. We should write small k in kilo abbreviation, because uppercase K is Kelvin (so kB is kilobyte and KB would represent to some people kelvinbyte, and that is just wrong unit).
The fact that IEC units "sound weird" isn't good enough reason to stick with SI units and prefixes with binary notation (base 2). If you don't like the name gibibyte than use something that won't be linked to real value of gigabyte, like "binary gigabyte".
Why should we decide which notation to use? Imagine that you are going to warehouse to buy some wooden planks of exact length of 10 'units', because you want them to fit exactly to what you are building. But, when you come back with planks, you notice that there is deviation in length of 7% (7% longer than you needed). Than you spend some time fixing these planks by making them shorter and than you realize you just bought one extra plank. Next day you go to another warehouse because first one from yesterday was closed. But, this time you are smarter and you buy planks of length 9.3 'units'. You arrive home and notice that now these are shorter than you hoped to be, because second warehouse was using different values. Now you have this ugly empty part in your built because of shorter planks. Fortunately, this is not happening in real life because units for length are defined. Why shouldn't this be case with memory units for capacity in computer systems?